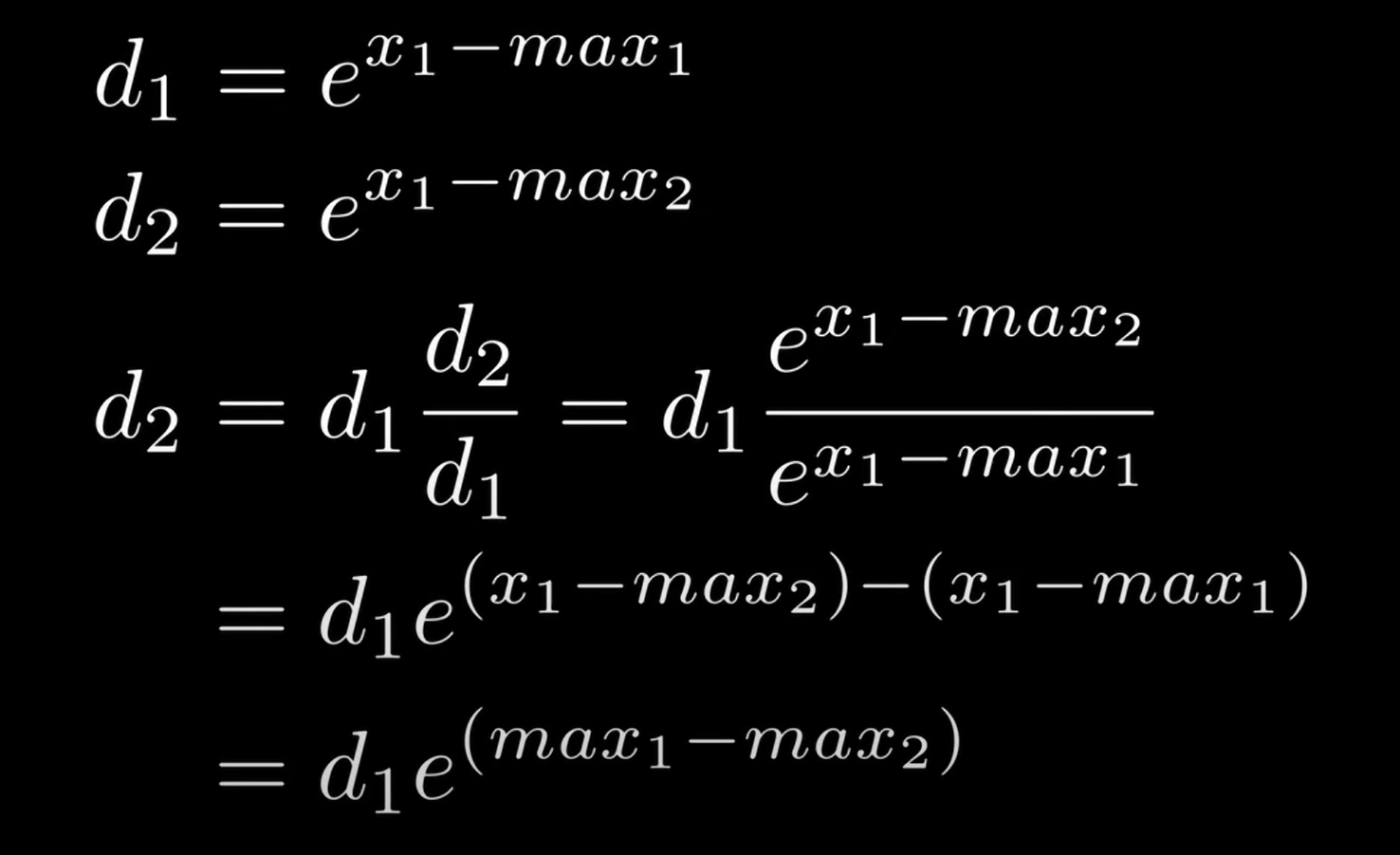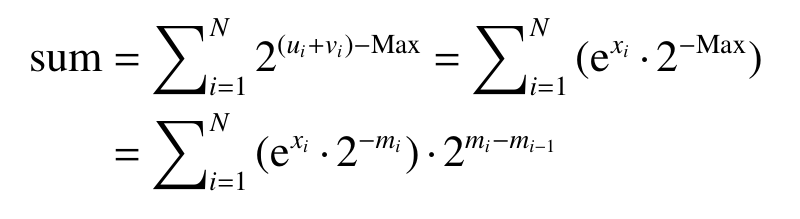硬件softmax

硬件友好的高效softmax函数实现调研与分析 - 知乎 Flash Attention中softmax分块计算详解 - 知乎

How to write a fast Softmax kernel

补充一点GPU背景知识：一个warp有多个线程，如果这些线程访问的地址相互之间拼接起来是连续的，那么GPU可以将这些请求合并为一次访存操作

1. 优化多线程访存，以及分块softmax的局部最大值（Fast Reduction）

__shared__ float reduction[BLOCK_DIM_Y];  
float maxval = FLOAT_MIN;
for (int i = ty; i<w; i+=BLOCK_DIM_Y)  {
  maxval = fmaxf(maxval, a[row*w + i]); 
} 
reduction[ty] = maxval;  
for(int stride = BLOCK_DIM_Y/2; stride>=1; stride/=2) {
  syncthreads(); 
  if (ty < stride)  {
    reduction[ty] = fmaxf(reduction[ty], reduction[ty+stride]);  
  } 
} 
syncthreads ();  
maxval = reduction[0]; 

//example
a[row*w + i]: [4, 1, 6, 3, 9, 2, 5, 8, 7, 0, 3, 5, 2, 10, 1, 4] 
线程数ty: 4 (0,1,2,3)  
- 线程0 计算: max(4,1,6,3) = 6 
- 线程1 计算: max(9,2,5,8) = 9 
- 线程2 计算: max(7,0,3,5) = 7 
- 线程3 计算: max(2,10,1,4)=10  
- 共享内存: reduction[0]=6, reduction[1]=9, reduction[2]=7, reduction[3]=10  
- 规约过程: 
- 第一轮(stride=2): - reduction[0]=max(6,7)=7 - reduction[1]=max(9,10)=10  
- 第二轮(stride=1): - reduction[0]=max(7,10)=10  

- 最终结果为10。

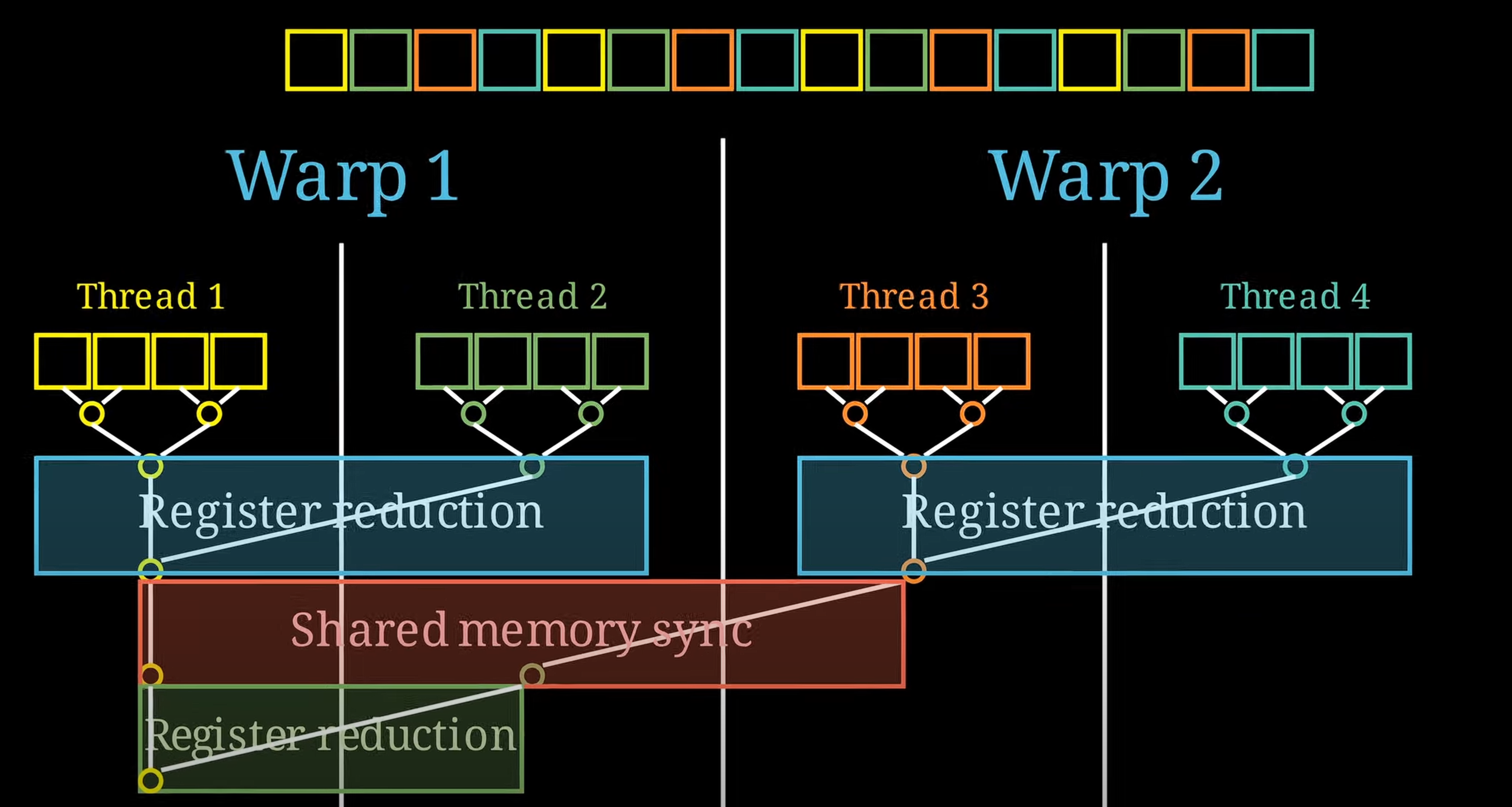
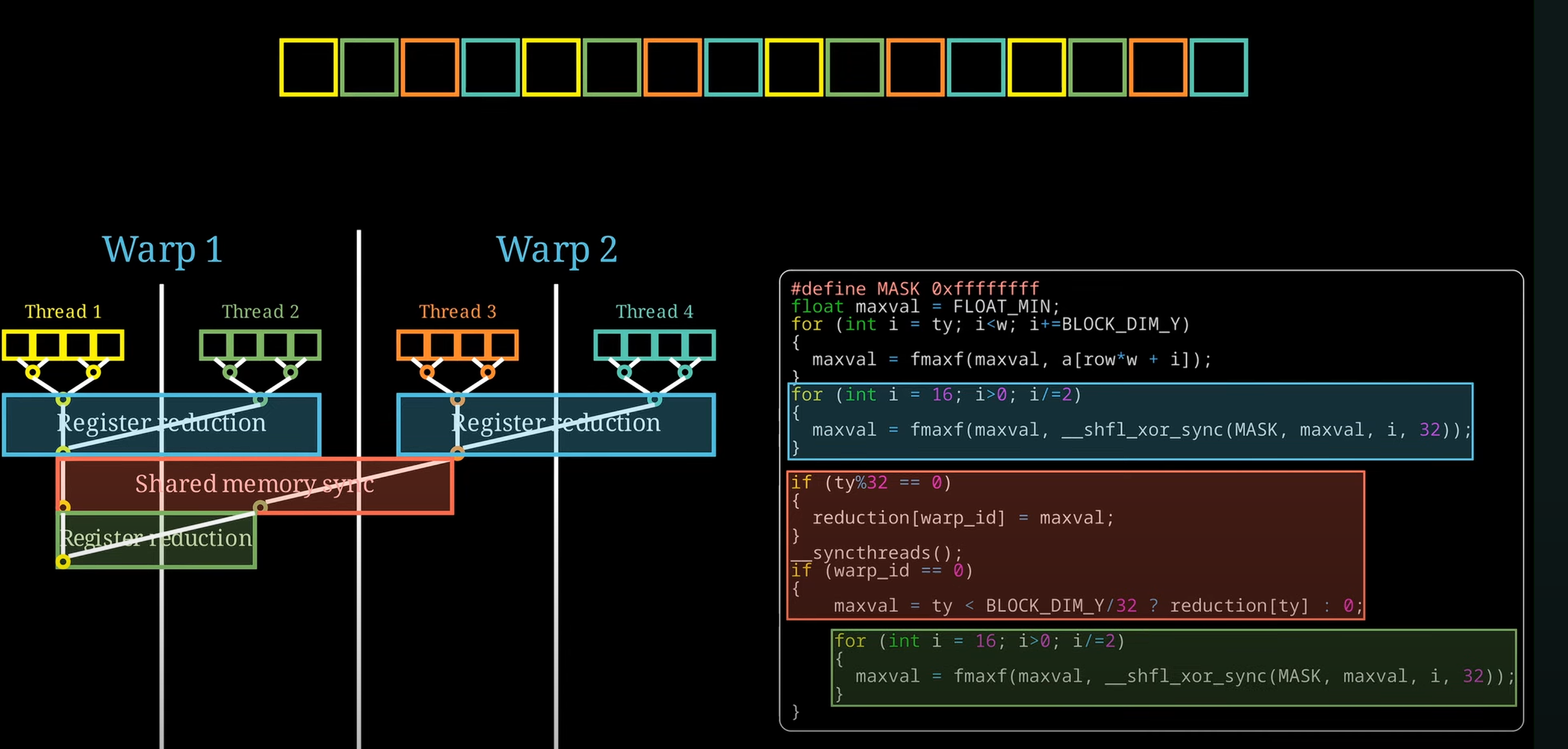
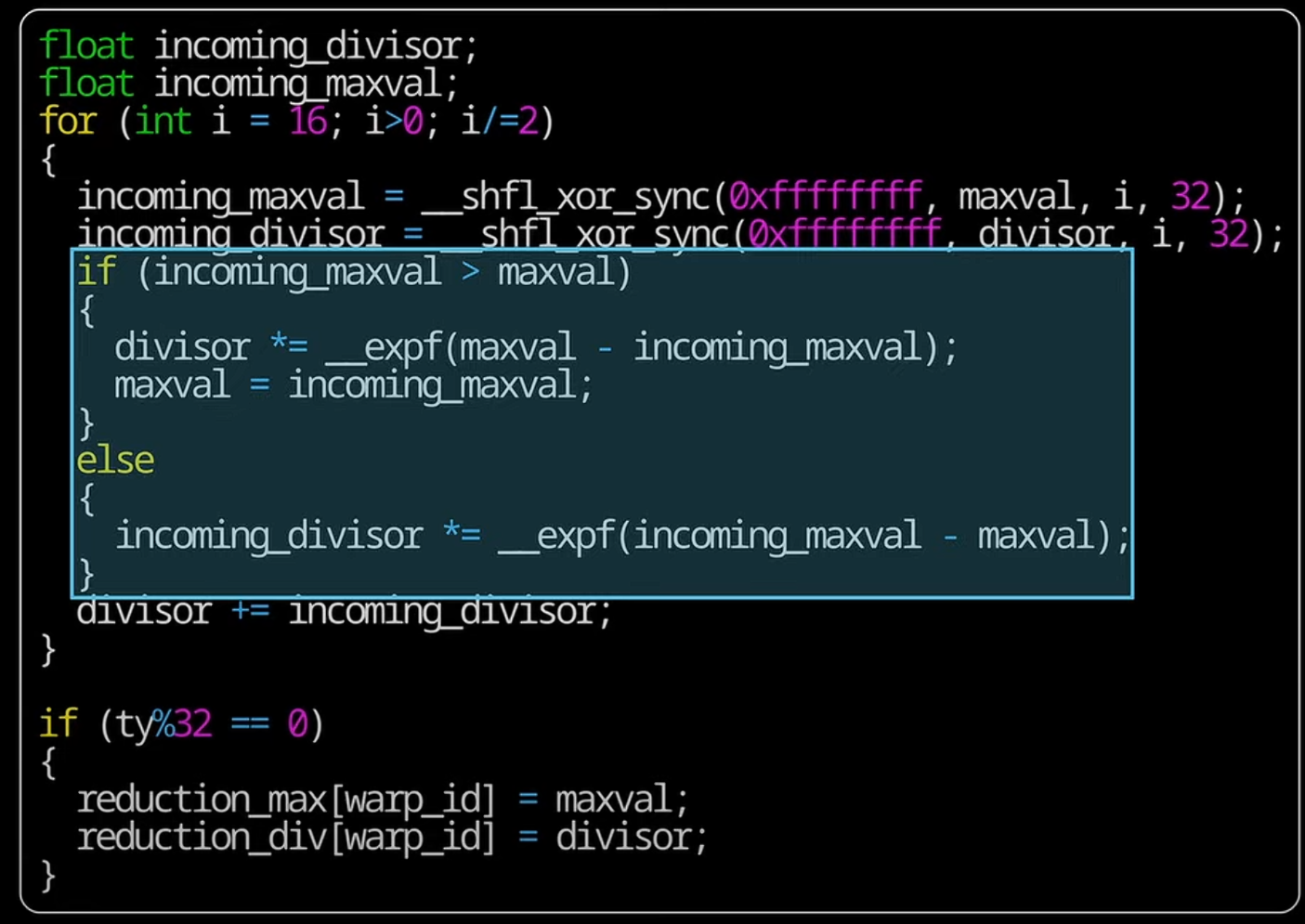
1. 局部最大值在wrap之间的同步优化（Register Reduction）

在GPU中，可以并行获取线程局部的最大值，然后需要考虑如何得出线程之间的最大值：在warp中获取最大值（寄存器层面），之后再同步warp之间的最大值（shared memory–shared cache）

BLOCK_DIM_Y是线程数，（在shared mem层面）只会调用warp1中的前面warp个线程来读取reduction[warp_id]，最后再在寄存器层面交换所有线程的maxval

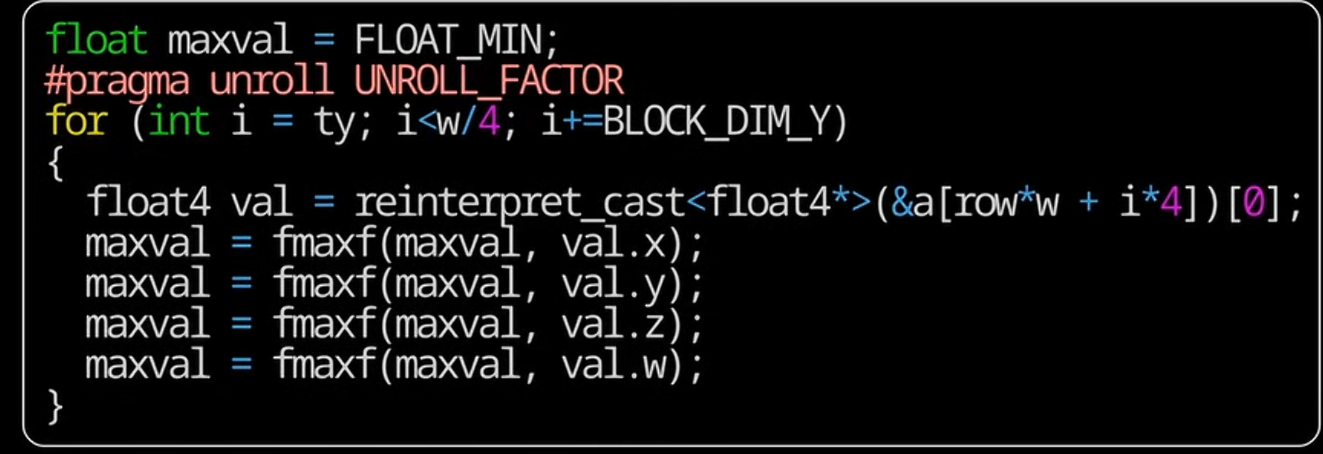
1. 利用fp4，加上unroll循环

如果我们写了 #pragma unroll 4 ，编译器会尝试把原本循环体写成4份接连执行，而不是每次循环都做一次比较、跳转等操作。

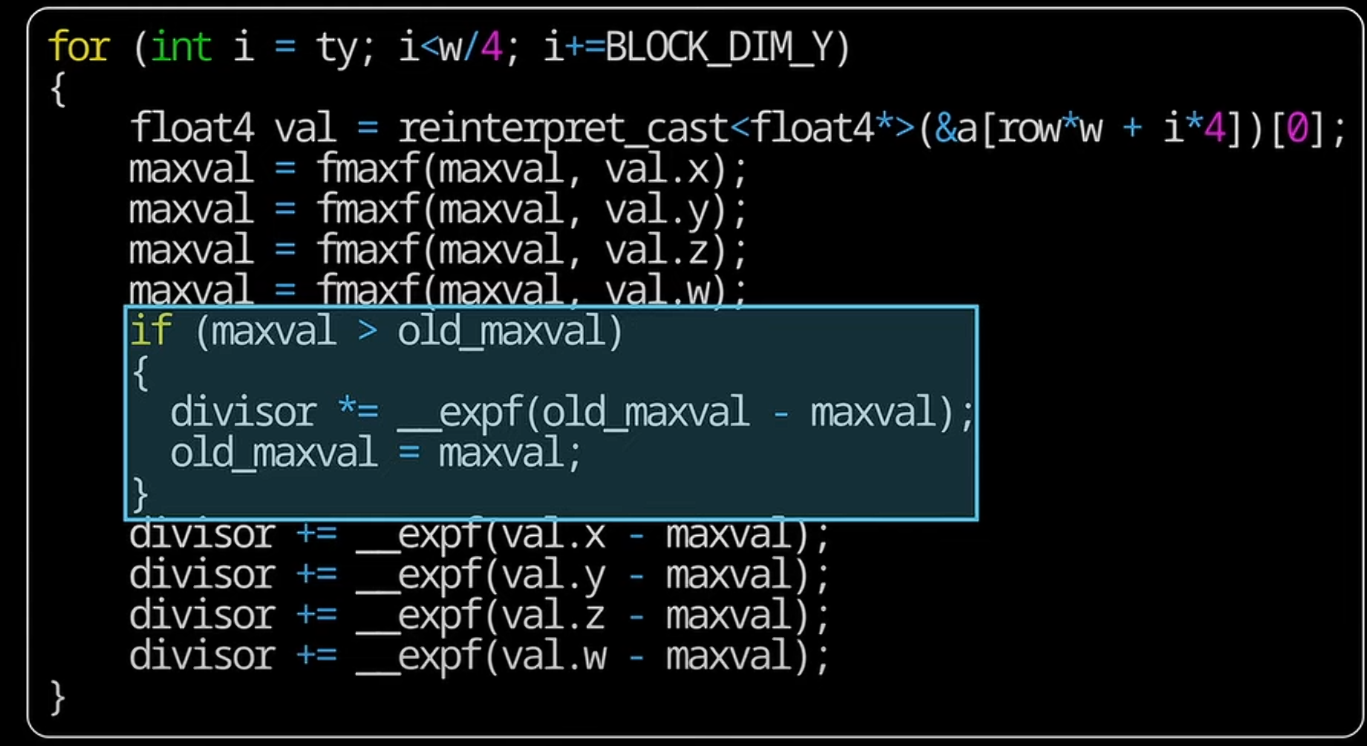
1. 继续优化访存，在求最大值和求分母divisor需要两次访存，需要做如下两步

如果找到了新的maxval，需要计算

divisor = divisor * expf(maxval - incoming_maxval) + incoming_divisor d_new+d_preall

如果比现有的最大值小，由于该进程的max并不是真的max 需要乘以一个$e^{maxlocal-maxval}$

divisor += incoming_divisor * expf(incoming_maxval - maxval) +=d_new

---

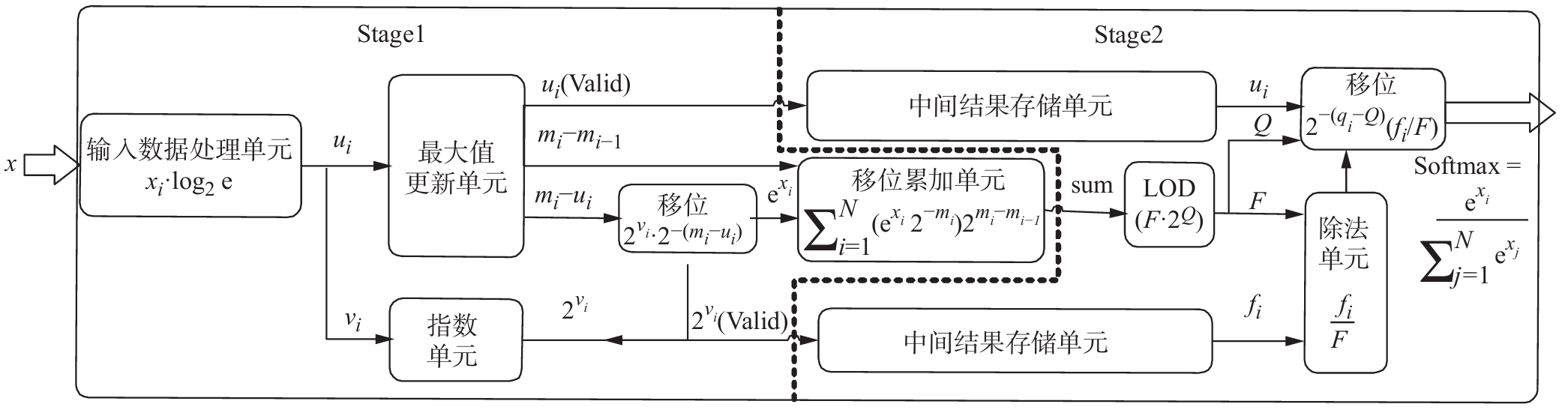
paper1：A High-Speed and Low-Complexity Architecture for Softmax Function in Deep Learning

\[\begin{align} s_i&=\dfrac{e^{x_i}}{\sum_{j=1}^N e^{x_j}} \\ &=exp(ln(\dfrac{e^{x_i}}{\sum_{j=1}^N e^{x_j}})) \\ &=exp(x_i-ln(\sum_{j=1}^N e^{x_j}))\\ &=exp(x_i-ln(F)) \end{align}\] \[lnF=ln2*\log_{2}^{F}\] \[\begin{align} e^{x_i}&=2^{x_i\log_{2}^{e}}=2^{u_i+v_i}\\ &=2^{v_i} << u_i (u_i>0)\\ &=2^{v_i} >> -u_i (u_i<=0)\\ \end{align}\]

对$x_i*\log_{2}^{e}$可以进行这样的优化：

$\log_{2}^{e}=1.0111_2=1+0.1_2-0.0001_2$，所以可以看作$A+A»1-A»4$

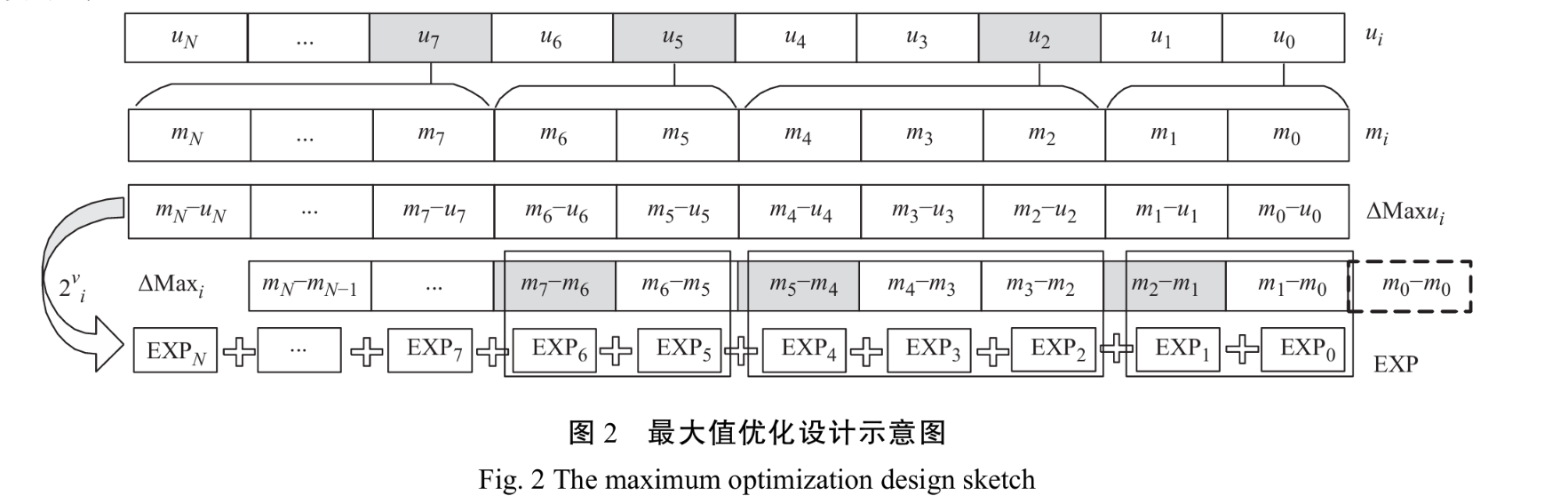
对$lnF$而言，存在一个$k \in [1, 2)$，满足$F=2^wk$，所以只要找出F中，从左到右第一个1的位置的数，记作index，$w+index=F.getwidth-1$，k是F移位后的结果。

$lnF=ln2(w+\log_{2}^{k})=ln2(w+k-1)$，LOD的输出是w，k=F»w

$ln2=0.1011_2=0.1+0.01-0.00001$，所以看作B»1+B»2-B»5

总结流程：

• 串行输入$x_i$，存下来。得出$u_i,v_i$，同时不断累加获得F
• 通过F经过LOD处理，得出w,k
• 取出$x_i$，对$x_i-ln2*(w+k-1)$处理获得$u’,v’$，得出$s_i$

注：这里的x是原始$x-x_{max}$

现在的问题就是得先等x都传输完了，才能算出w,k，然后又得慢慢取出x，算si。效率太低了

##

---

这个文章好像是假的，我复现出来的结果不对

本文首先对Softmax函数计算进行优化，采用稀疏化策略，只选择输出有效值进行指数计算和存储，以降低计算冗余和存储需求； 其次通过动态移位更新最大值的方式，将最大值求取隐藏在流水线中，以提高计算效率。另外，依据 Softmax精度需求，指数及除法计算单元可配置成不同的设计方案，通过改进分段线性拟合算法，可 实现通用非线性函数中的指数、除法及S型函数等计算操作，缩小硬件资源开销。

\[e^{x_i}=2^{x_i\log_{2}^{e}}=2^{u_i+v_i}\] \[\begin{align} s_i&=\dfrac{e^{x_i}}{\sum_{j=1}^N e^{x_j}} \\ &=\dfrac{2^{u_i+v_i-max}}{\sum_{j=1}^N 2^{u_i+v_i-max}} \\ &= \dfrac{2^{v_i}2^{-(max-u_i)}}{sum} \\ (_LOD)&=\dfrac{f_i2^{-q_i}}{F2^Q} \end{align}\]

上面讲解了如何算出sum来，然后根据sum，设计一个LOD，来推断出一个$F \in [1, 2)$以及Q ,需要存储输入的$u_i和2^{v_i}(即f_i)$

硬件上：