Digit-Serial 脉动结构(Systolic)的乘法器
Digit-Serial 脉动结构(Systolic)的乘法器
1. 概念的介绍
对于有限域 $GF(2^n)$,设其模多项式为
\[m(x) = x^n + \sum_{i=0}^{n-1} m_i x^i \quad (m_i \in \{0,1\}),\]则满足以下公式:
\[x^n \mod m(x) = [m(x) - x^n] = \sum_{i=0}^{n-1} m_i x^i\]设有限域 $GF(2^n)$上的任意两个多项式 A(x)、 B(x) 以及既约多项式 G(x) 分别为:
\[A(x) = a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \cdots + a_1x + a_0,\] \[B(x) = b_{n-1}x^{n-1} + b_{n-2}x^{n-2} + \cdots + b_1x + b_0,\] \[G(x) = x^n + r(x) = x^n + g_{n-1}x^{n-1} + g_{n-2}x^{n-2} + \cdots + g_1x + g_0,\]其中,$a_i, b_i, g_i in GF(2^n)$。
设 A(x) 与 B(x) 的乘积 P(x)为:
\[P(x) = [A(x) \cdot B(x)] \mod G(x) = p_{n-1}x^{n-1} + p_{n-2}x^{n-2} + \cdots + p_1x + p_0,\]则:
\[P(x) = A(x) \cdot \left(b_{n-1}x^{n-1} + b_{n-2}x^{n-2} + \cdots + b_1x + b_0 \right) \mod G(x).\]展开可得:
\[P(x) = \left\{\cdots \left[A(x) \cdot b_{n-1}x^{n-1} \mod G(x) + A(x) \cdot b_{n-2}x^{n-2} \mod G(x)\right] \cdots + A(x) \cdot b_1x \mod G(x) + A(x) \cdot b_0 \right\}.\]由上述公式可知,有限域 $GF(2^n)$上的多项式运算可以通过选代完成,选代单元为:
\[T^{(i)} = T^{(i-1)} \cdot x \mod G(x) + b_{n-i}A(x), \quad 0 < i \leq n,\]其中:
\[T^{(0)} = 0, \quad T^{(n)} = P(x).\]实际上,选代单元 $T^{(i)}$ 也是有限域 $GF(2^n)$ 中的多项式元素,令:
\[T^{(i)} = t_{n-1}^{(i)}x^{n-1} + t_{n-2}^{(i)}x^{n-2} + \cdots + t_1^{(i)}x + t_0^{(i)},\]则
\[T^{(i-1)} = t_{n-1}^{(i-1)}x^{n-1} + t_{n-2}^{(i-1)}x^{n-2} + \cdots + t_1^{(i-1)}x + t_0^{(i-1)}.\]由选代关系可以推得:
\[T^{(i)} = T^{(i-1)} \cdot x \mod G(x) + b_{n-i}A(x)\]展开为:
\[T^{(i)} = \left[ t_{n-1}^{(i-1)}x^{n-1} + \cdots + t_1^{(i-1)}x + t_0^{(i-1)} \right]x \mod G(x) + b_{n-i}A(x)\]即:
\[T^{(i)} = \left[ t_{n-1}^{(i-1)}x^n + \cdots + t_1^{(i-1)}x^2 + t_0^{(i-1)}x \right] \mod G(x) + b_{n-i}A(x).\]由此可得:
\[T^{(i)} = t_{n-1}^{(i-1)} \cdot r(x) + t_{n-2}^{(i-1)}x^{n-1} + \cdots + t_1^{(i-1)}x^2 + t_0^{(i-1)}x + b_{n-i}A(x).\]分项展开为:
\[T^{(i)} = \left[t_{n-1}^{(i-1)}g_{n-1} + t_{n-2}^{(i-1)} + b_{n-i}a_{n-1}\right] \cdot x^{n-1}\] \[+ \left[t_{n-1}^{(i-1)}g_{n-2} + t_{n-3}^{(i-1)} + b_{n-i}a_{n-2}\right] \cdot x^{n-2}\] \[+ \cdots\] \[+ \left[t_{n-1}^{(i-1)}g_1 + t_0^{(i-1)} + b_{n-i}a_1\right] \cdot x^1\] \[+ \left[t_{n-1}^{(i-1)}g_0 + b_{n-i}a_0\right] \cdot x^0.\]即:
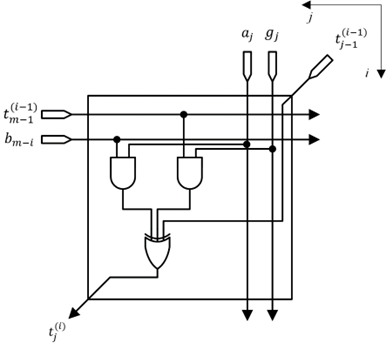
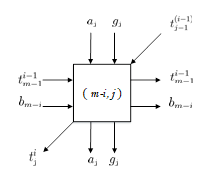
\[t_j^{(i)} = t_{n-1}^{(i-1)}g_j + t_{j-1}^{(i-1)} + b_{n-i}a_j,\]其中 $1 \leq i \leq n$ 且 $t_i^{(0)} = 0, t_{-1}^{(i)} = 0$
则 $A(x)$ 与 $B(x)$ 的乘积 $P(x)$ 为:
\[P(x) = T^{(n)} = \sum_{j=0}^{n-1} t_j^{(n)}x^j.\]考虑到上述各参数均处于有限域$GF(2^n)$中,因此其均为0或1,上式中乘法可以用与门实现,加法可以用异或门实现
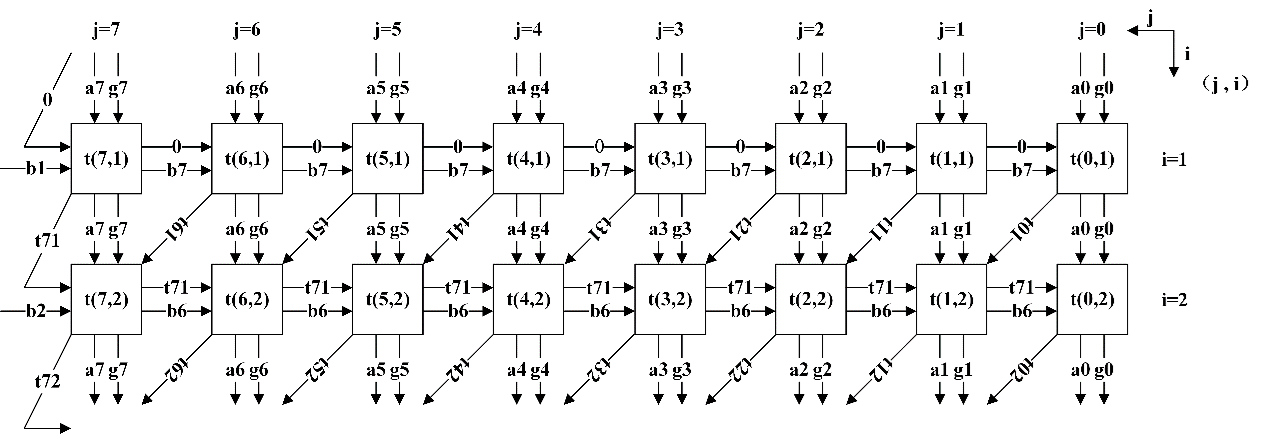
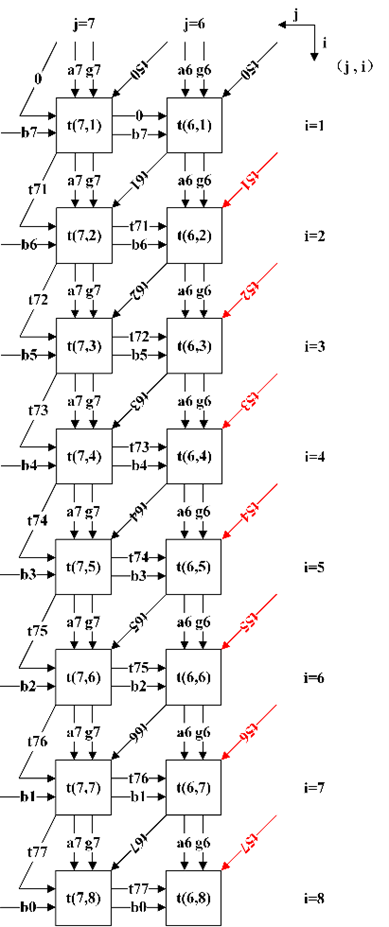
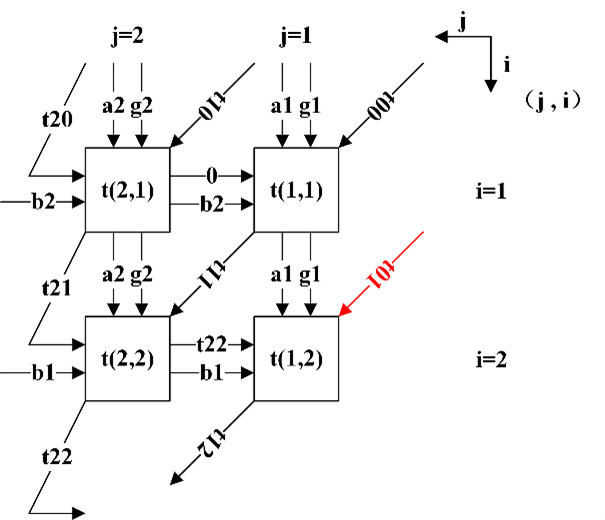
假设n为8, Bit-Parallel阵列形式如下,这是一种并行度最高的架构。
This post is licensed under CC BY 4.0 by the author.